Constraints

A constraint on a set of variables means a predicate defined on them that is imposed. The extension of the constraint gives the permitted values of the variables.

For example, consider real-valued variables x and y with the constraint

    x2 + y2 = 1.

The extension of this constraint is:

    { (x,y) | x2 + y2 = 1 }

In a relational database, constraints are often defined on the relation variables (relvars). These are called declared constraints. Examples are uniqueness, key, inclusion and referential integrity constraints.

Usually constraints are imposed on the base relvars, by aborting transactions that attempt updates that violate the declared constraints.

Data integrity

Constraints are great for ensuring data integrity.

The C in ACID transactions stands for consistency (see Consistency (database systems) []). Consistency is often defined to mean database constraints are not violated.

Many people praise data integrity.

For example Chris Brook in his blog post What is Data Integrity? Definition, Best Practices & More (Jan 2019) says:

For modern enterprises, data integrity is essential for the accuracy and efficiency of business processes as well as decision making. It’s also a central focus of many data security programs. Achieved through a variety of data protection methods, including backup and replication, database integrity constraints, validation processes, and other systems and protocols, data integrity is critical yet manageable for organizations today.

Philippe Charbon, in his article Data Integrity: A Return to Basics (Jan 2018) says:

It is therefore that we arrived at a crucial turning point where one has to return to the fundamental value of ensuring that your company's data is accurate and reliable. And this is for good.

Here are just some of the advantages of imposing constraints:

• Forces users to be careful, and to fix errors at the time information is entered, not later
• Avoids errors in the data
• Data model is simpler
• Indexing more efficient (for example a key constraint implies an index on that key only maps to a single tuple
• Queries are simpler

Disadvantages of imposing constraints

But there are many disadvantages with imposing constraints:

• Can't record partial information
• Prevents real-time interactive collaborative data entry
• Less concurrency
• Less logical independence
• More dead-locks
• Poor writer performance
• Updates are complex
• Updates are fallible
• Need compensating actions
• Multi-master replication and synchronisation using Operational Transformation is intractable
• Prevents configuration management involving branching and merging
• Draft data (work in progress) tends to exist in transient "temporary" variables (e.g. as a data entry form is filled by a user) and not managed by the DBMS
• Optimistic concurrency control and retry loops tend to be needed for data entry
• Cannot record conflicting information
• The recorded information lacks fidelity
• Unrealistic
  • Users are not omniscient
  • Users make mistakes
  • Updates are asynchronous
• There is no information about the quality of the data. There can be a false sense of security

Applications for editing data with complex constraints complicates application code, and gives a poorer user experience. Contrast with applications to edit unconstrained data.

Dealing with integrity constraints

Both the advantages and disadvantages are pretty compelling. It seems unfortunate to pick one or the other. But actually there's no need for a trade-off at all! There's a simple solution where we get our cake and eat it too: apply constraints indirectly. The idea is shown in the following diagram:

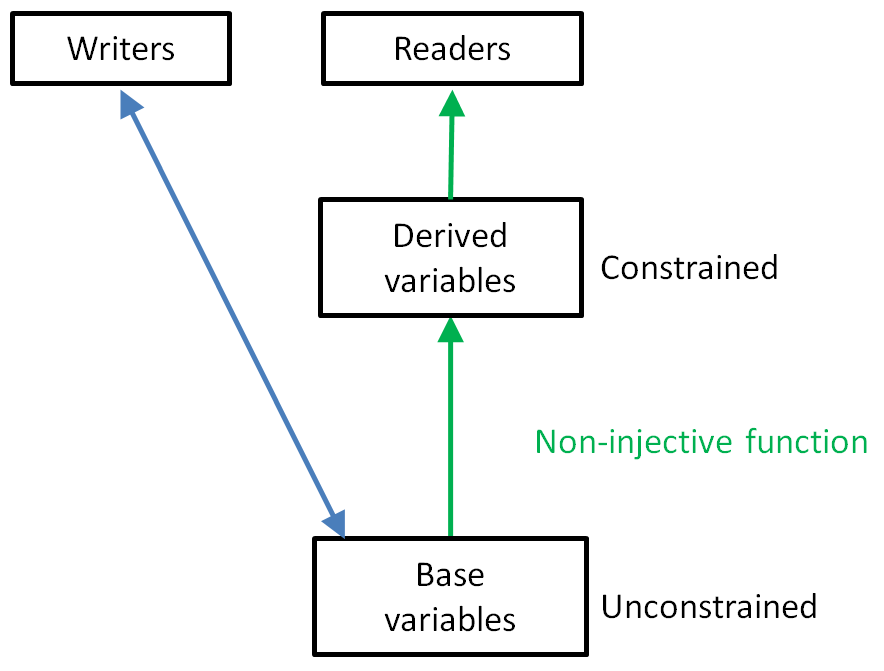
Writers access a base representation which is relatively unconstrained. Update operators tend to be simple and infallible. From the point of view of the writers, satisfying a complicated constraint is made easy, rather than it being difficult to achieve and making writes fragile. Users are able to drive the output through a complicated space.

A function maps the base representation to a read-only derived representation which imposes the constraints. For efficiency the derived variables are typically updated with incremental computing. This function may not be injective []. That means that the base representation isn’t canonical. There can be significant advantages to not imposing canonical representations. Canonical representations often seem arbitrary (because they break symmetries). E.g. a represention of a triangle as an array of three vertices isn't canonical because triangles are invariant under cyclic permutations of their vertices.

An important consideration is the choice of what variables to materialise.

This approach tends to mean writers have very low computation load and tend to access only a small number of the base variables. This is a good thing when Multi Version Concurrency Control (MVCC) is used, because writers are serialised when they access the same base variable (so it's good they they only lock resources for a small time) whereas readers can run in parallel.

The Jigsaw derived representation provides an example of how Operational Transformation can be used on an unconstrained base representation and yet a derived representation imposes constraints on the relative positions of the jigsaw pieces as they are snapped together.

Unconstrained base variables makes it easier to achieve logical independence for writers. This allows for applications that access a database to be immunised from database schema changes. In other words, imposing constraints indirectly solves many view update problems, such as an insertion into a restriction.

Integrity constraints tend to increase the complexity of update operations. A popular solution is to use compensating actions. However it's better to impose constraints indirectly in the manner discussed here.

As an example, key constraints can be dealt with in this way.

This approach could be regarded as CQRS (Command-Query Responsibility Segregation).

Asynchronous reads, stale reads, MVCC, snapshot isolation, multi-slave

The idea that readers are able to see stale versions of the data (because of MVCC) fits well with the tendency for the readers themselves to take a time to calculate their values, perhaps because of the high computational load, and/or the large number of base variables which need to be read. It makes sense for readers to use asynchronous I/O and to also execute the computational tasks asynchronously, typically by posting them to a thread pool.

This technique fits in well with multi-slave systems, allowing readers to scale without limit.

Derived variables on multiple sources

Materialising derived variables makes them available. It is possible for a read database to represent a derived variable based on multiple write databases. It can collate the information and present it. For each source it can use persistent queues, vector times etc to achieve EOIO processing of the updates on the sources, allowing for the read database to be maintained.

Other advantages

The derived variables can be regarded as a view of the data.

Some other advantages of this approach, not already mentioned:

• Better control over security and data access rights
• Fits well with data warehousing
• Reactive programming
• High performance stream processing. Stream processing [] simplies parallelism by allowing for a pipeline to be used to process items in a FIFO queue. Derived variables are typically calculated as an aggregate over records in the base data. This is well suited to high performance stream processing. This includes ability to stream updates on writer database to reader database(s). This depends on EOIO processing of the updates.
• Scalability There are massive performance benefits to both readers and writers. It is easier to scale up both. Unconstrained writers allows for separation into parts which can be updated independently. Readers can scale up because they use parallelisable stream processing.
• Missing information The predicates in the write schema tends to be simpler and more orthogonal when one doesn't have to worry about read performance. The write schema can avoid NULLs, instead use lots of simpler predicates, which allow for partial information to be recorded.
• Optimise read and write performance at the same time
• Multiple read databases Allows for multiple read databases each with their own read schema. Read schema can have less information. Can be optimised for a service that needs that data. A read schema can be owned by another service.
• Handles spikes in operation throughput The write schema is unconstrained, avoids redundancy, avoid secondary indexes and avoids computation. Therefore is allows for very high write rates. Writers can easily cope with the peaks for operation throughput. E.g. short term spikes, day versus night, or black friday sales periods. In some systems the peak is much higher than the average. The readers can calculate in the background, a spike might increase lag, but readers are eventually consistent with writers.
• Availability of services
• Fits well with an events database
• Promotes avoidance of race conditions

Intractable problems versus easy problems

The following problems are conceptually straightforward software "engineering" problems:

• imposing constraints for readers using non-injective functions
• logical view independence for readers
• parallelism for readers
• data replication for readers

Depending on the constraints the following problems can be so difficult they're impossible or intractable:

• in-place multi-user data entry
• useful and sufficient update operations that avoid constraint violations
• update operations that commute
• view update problem
• correct and efficient update anywhere anytime (multi-master) replication
• Operational Transformation satisfying TP1 and TP2

The correct approach is to relax constraints because it avoids the intractable problems and one is left with straightforward engineering problems.

What constraints are we talking about?

Most constraints! For example:

• constraints preventing the recording of partial information or conflicting information
• key constraints in general
• inclusion dependencies in general
• Number of registered players cap or a salary cap on a sports team
• Objects in drawing don't intersect
• Objects in drawing are connected
• Layout constraints on VLSI chips
• Output fan-out constraints on digital circuits
• Constraints imposed on a string such as maximum size, or that it conforms to a grammar