Key constraint

A candidate key [] of a relation is a minimal superkey for that relation.

In the following we illustrate the idea of imposing constraints indirectly for the case of a key constraint.

Relaxing a key constraint allows for recording conflicting information. That means the DBMS can merge edits and keep the conflicting information, allowing the users to fix it up as appropriate.

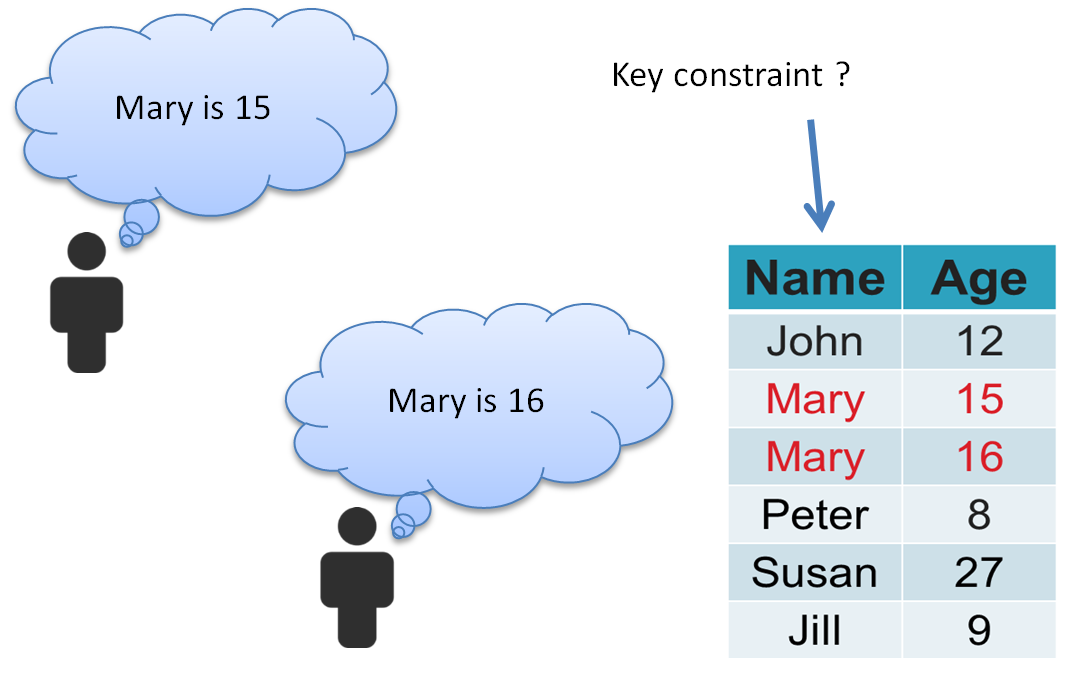
Imposing a key constraint indirectly solves view update problems, such as an insertion into a restriction.

Example

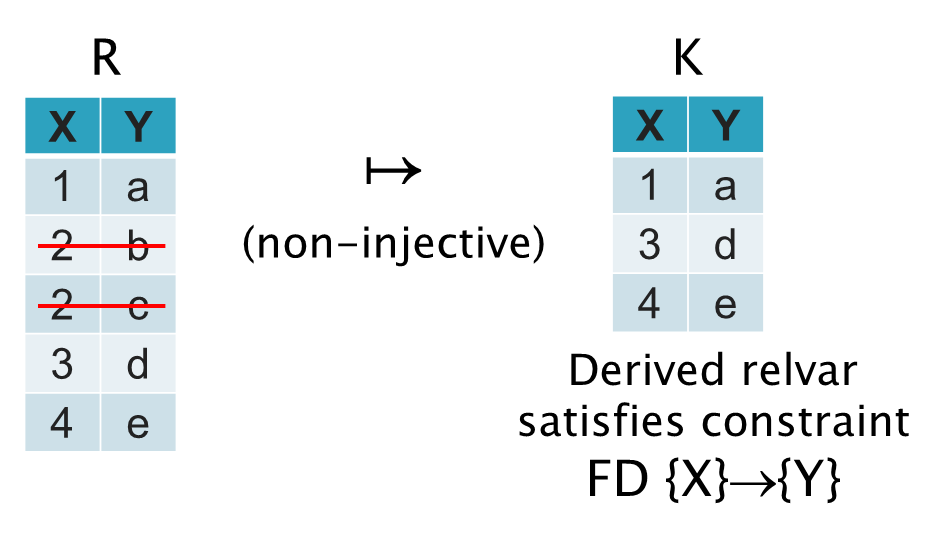
Consider the following relation R which violates the FD: {X}→{Y} (see functional dependency []).

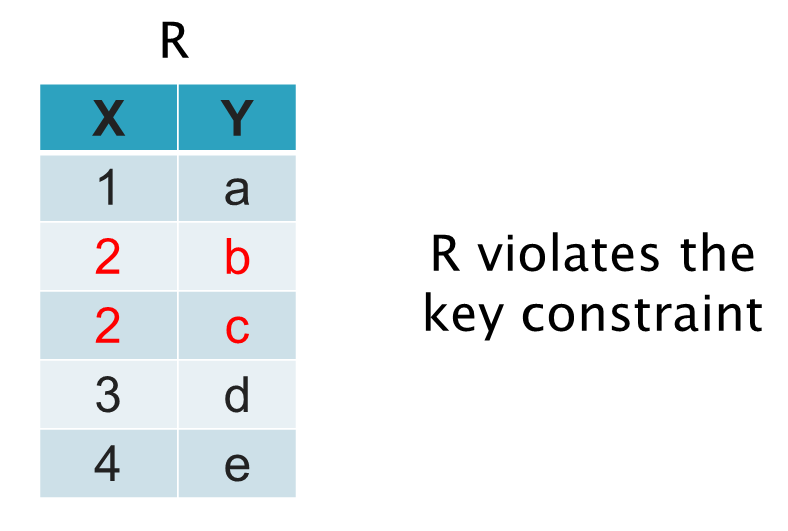
We would like to impose the key constraint expressed by the FD {X}→{Y}, but only indirectly.

Remove duplicates to satisfy the key constraint

Consider that a derived variable K is defined using a relational algebra expression on R such that K contains the tuples from R without the duplicates.

Therefore K satisfies the key constraint:

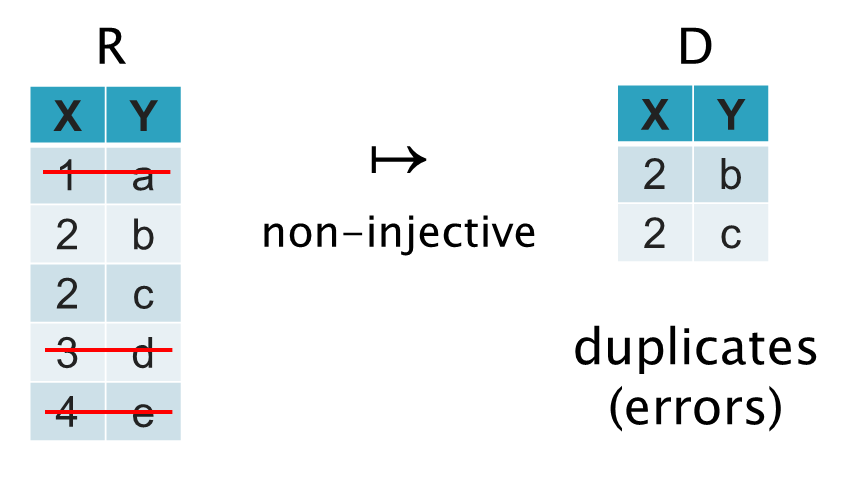
Can derive the offending tuples (highlight "errors" to users)

Consider that a derived variable D is defined using a relational algebra expression on R such that D contains the duplicates from R:

Can materialise a bijective representation

There is a bijection between R and (K,D). Therefore we can consider the pair (K,D) to be an alternative representation of the information in R.

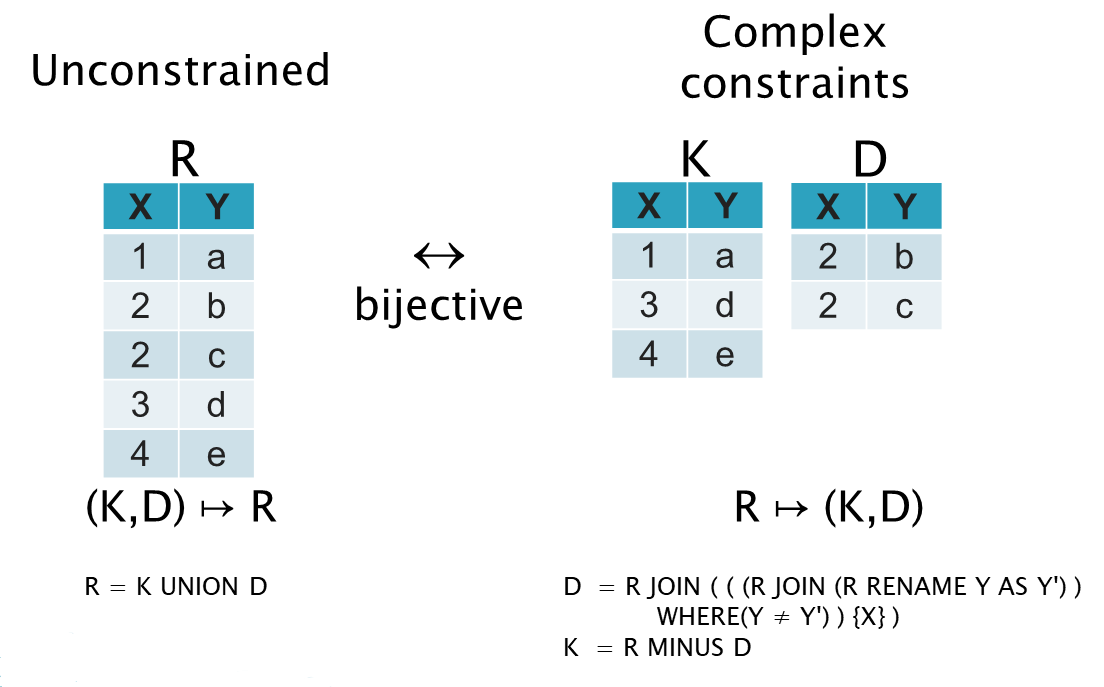
Indeed it is appropriate for the physical implementation to materialise the representation (K,D) instead of R, because it is cheaper to calculate R from (K,D) rather than the reverse.

Nevertheless R is regarded as the more appropriate representation for expressing updates, since it is unconstrained, whereas (K,D) have complicated constraints.

The representation R is also more appropriate for allowing Operational Transformation to be used to merge concurrent updates.

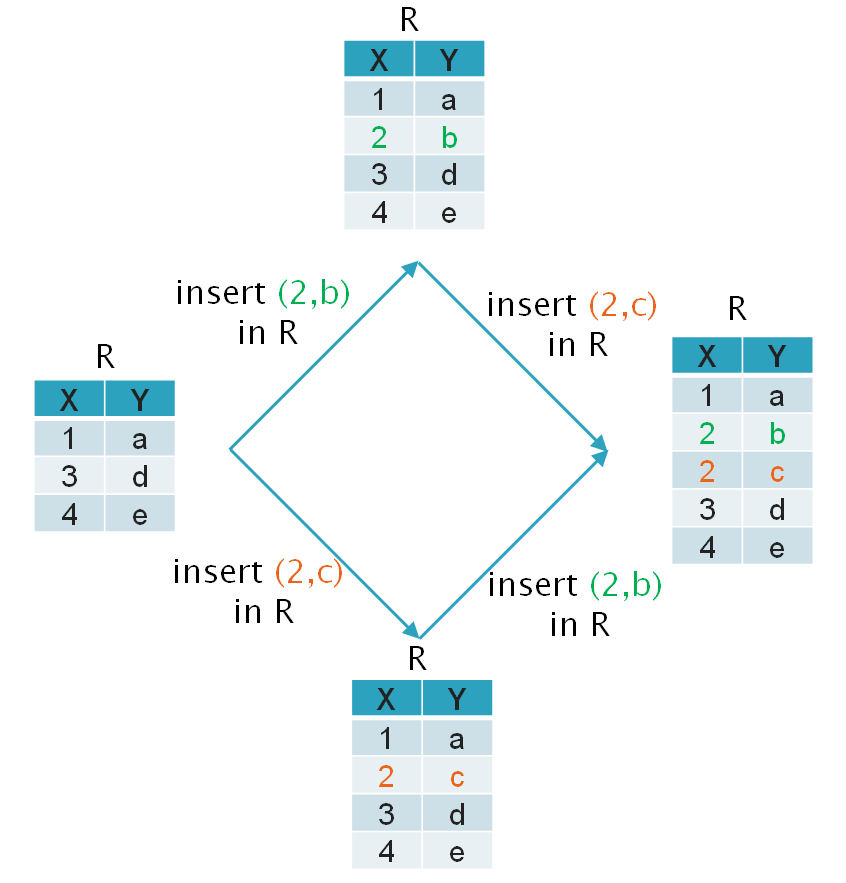
Operational Transformation on R

Since R is unconstrained, it is relatively easy to merge concurrent operations. For example, insert operations on sets commute, so therefore:

Operational Transform on (K,D)

Much of the literature on Operational Transformation is concerned with finding inclusion transforms that satisfy properties TP1 and TP2, which are needed to ensure all sites converge at quiescence. See this primer on Operational Transformation

It is not easy, indeed there have been many examples of erroneous algorithms, one research group proposed using automated theorem provers to validate the solutions. See Proving correctness of transformation functions in collaborative editing systems by Gérald Oster, Pascal Urso, Pascal Molli and Abdessamad Imine (2005).

Trying to make Operational Transformation work with updates on K,D directly, while satisfying the transformation properties TP1 and TP2 appears like a hard problem, the solution indeed looks complicated:

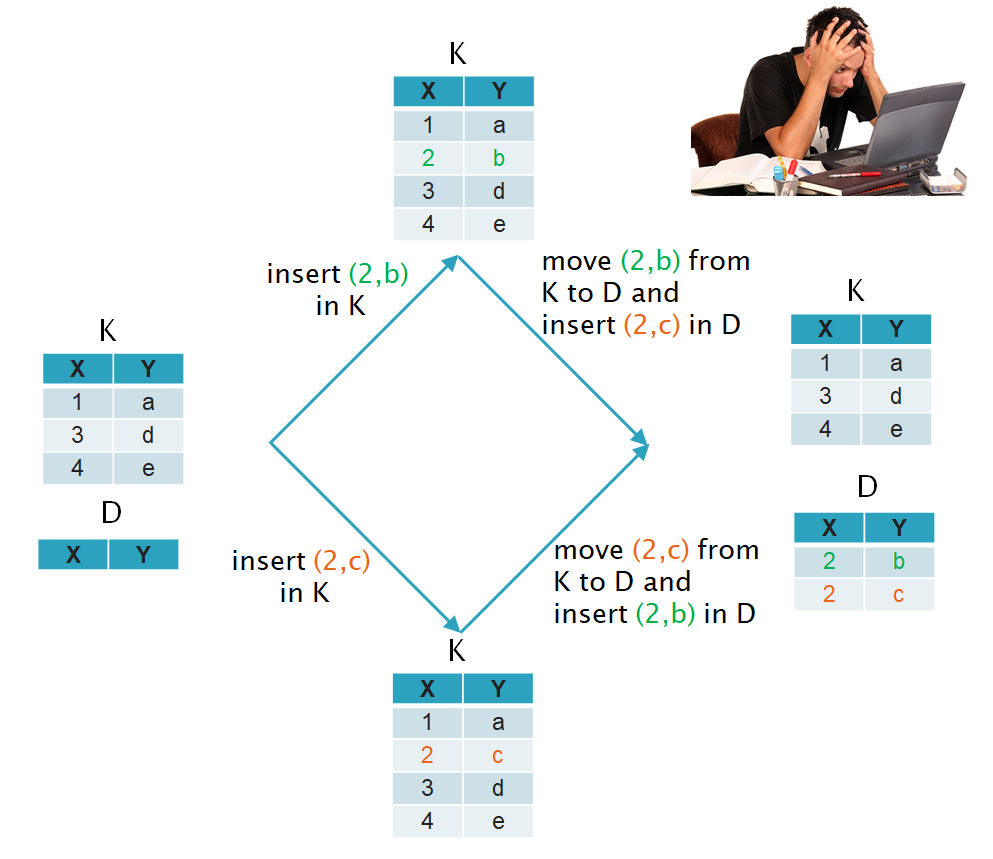
Note for example that inserting a tuple in R might do something relatively complicated on K and D. E.g. it may cause a tuple to be moved from K to D (a tuple is removed from K and two tuples are inserted in D). The math leads to interesting update operations on the representation using K,D in such a way that the FD constraint on K is imposed even as we merge concurrent operations.

Empty key

Declaring a relvar to have an empty key imposes the constraint that its cardinality doesn't exceed one. A relvar with an empty key cannot have any other keys defined - because it is never the case that a candidate key is a strict subset of another candidate key (candidate keys are irreducible).