Non-canonical representations

Consider the case of representing a rational number using a pair of integers. We have to decide whether or not to impose a unique representation (i.e. a canonical representation).

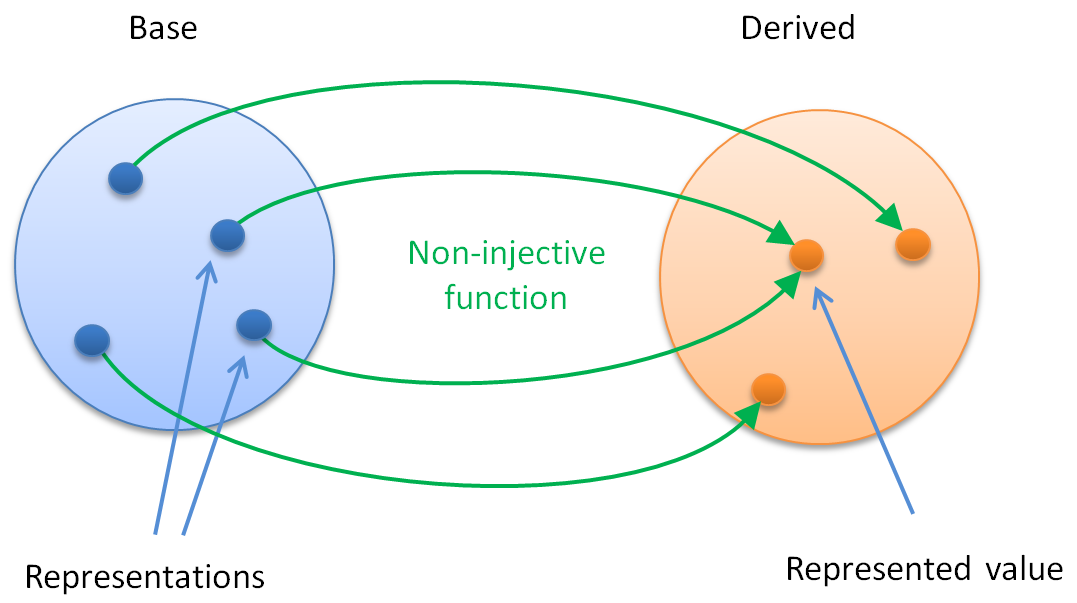
If the base variables in a database record non-canonical (i.e. non-unique) representations of the values they are intended to represent, then we can think of the represented values as being recorded in read-only derived variables which involve non-injectve functions of the base variables.

Representation of a rational number with strong constraints

A canonical representation of a rational number with a pair of integers \((n,d)\) can be achieved with the constraint

$$d>0 ∧ ((n=0 ∧ d=1) ∨ coprime(|n|,d))$$

The constraint can be illustrated by drawing dots at the coprime positions:

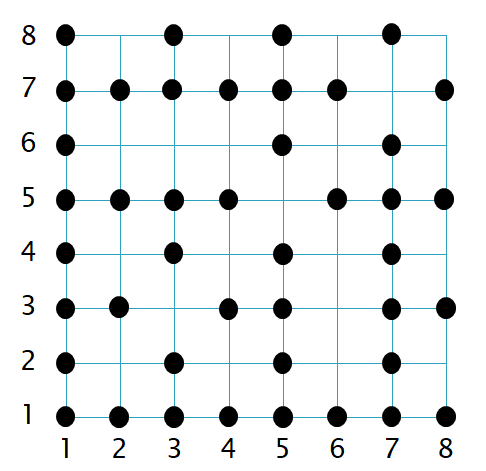
Clearly the extension of this constraint cannot be Cartesian factorised. Therefore \(n\) and \(d\) cannot be updated independently.

There is a bijection [] between the representation and what is represented. That is, between

$$\{(n,d)∈ℤ^2 | d>0 ∧ ((n=0 ∧ d=1) ∨ coprime(|n|,d))\}$$

and the rationals \(ℚ\).

Representation of a rational number with weak constraints

We can weaken the constraint so that the representation of a rational number using a pair of integers \((n,d)\) is non-canonical. For example there are multiple representations of the rational number 2/3.

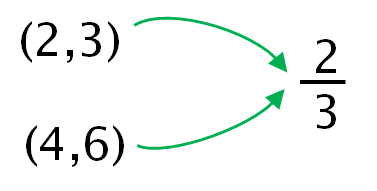
This means the mapping from the representation to what is represented is non-injective []

The extension of the constraint can be expressed as a Cartesian product \(ℤ \times ℤ\\\{0\}\). Therefore \(n\) and \(d\) can be updated independently.

An equivalence relation can be defined on the representation, according to whether the same value is represented:

$$(n_1,d_1) \sim (n_2,d_2) \mathrm{\ \ if\ \ } \frac{n_1}{d_1} = \frac{n_2}{d_2}$$