Matches function to check whether the dbvar has a given dbvalue
In the following it is shown we can construct a relational algebra expression to test whether the dbvar exactly matches a given dbvalue in schema `S`.
Given a relation `r` and a set of attributes `a`, let `π_a(r)` denote the projection of `r` onto `a`.
Note that `π_ϕ(r)` denotes the projection of r onto the empty set of attributes and
gives DUM if `r` is empty, otherwise DEE.
Given a relation `r`, let `empty(r) =` DEE`\\ π_ϕ(r)`.
This gives DEE if `r` is empty otherwise DUM.
Given union compatible relations `r` and `s`, let `r△s = (r\\s) ∪ (s\\r)` denote the
symmetric difference [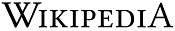 ].
].
Let `eq(r,s) = empty(r△s)`. This evaluates to DEE if r=s, otherwise DUM.
Let `d[R]` denote the value of relvar `R ∈ relvars(S)` in database value `d ∈ C(S)`.
Given database value `d ∈ C(S)`, let `matches(d) = ⋈ { eq(R,d[R]) | R ∈ relvars(S) }`
denote a relational algebra expression which evaluates to DEE if the dbvar
for schema `S` has value `d`, otherwise DUM.