Operational Transform Control Algorithms

Operations

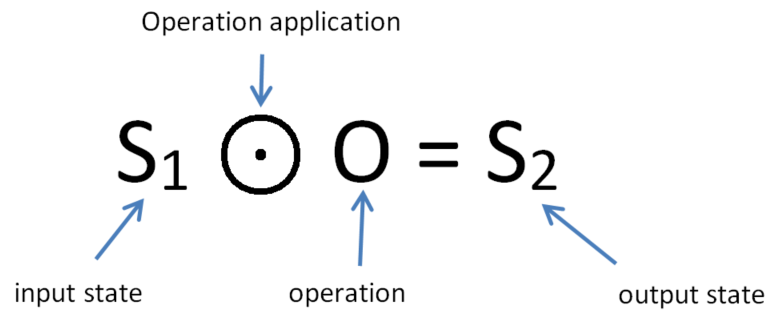
Operations represent the updates or deltas to be applied to the database. Let operation O be applied on state S₁ to get state S₂.

An example might be the deletion of a character within a string variable:

We call S₁ the input state and S₂ the output state of operation O. This state of affairs is expressed in the following equation:

Operations don’t necessarily commute

Function composition is associative but not commutative.

Associative: (f∘g)∘h = f∘(g∘h)

Commutative: f∘g = g∘f

Similarly operations don't commute in general, meaning they can't generally be applied in different orders.

Definition: We say O₁, O₂ commute if S ⊙ O₁ ⊙ O₂ = S ⊙ O₂ ⊙ O₁

Context equivalent and context serialised operations

Let O₁, O₂ be concurrent operations (i.e. O₁ || O₂).

Definition: We say operations O₁ ,O₂ are context equivalent if they share the same input state.

Definition: We say operations O₁ ,O₂ are context serialised if the output state of O₁ is the input state of O₂.

Transforms

Inclusion Transformation (IT)

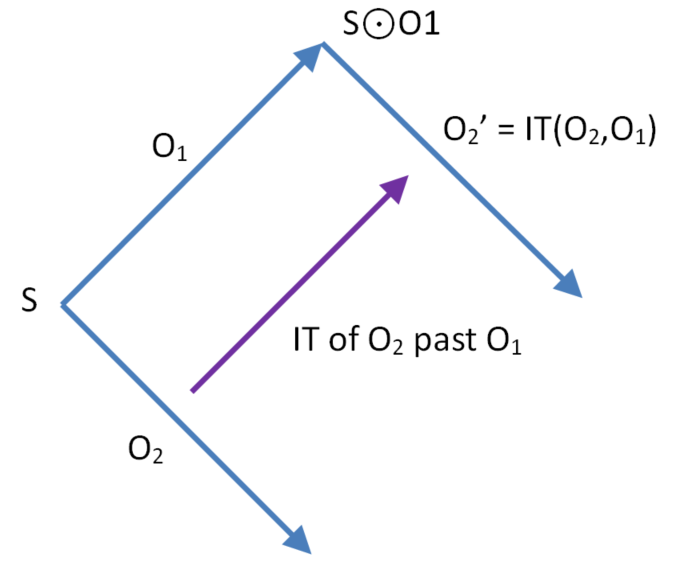
Let O₁ ,O₂ be context equivalent operations with input state S. The following diagram depicts the inclusion transform of O₂ past O₁ to give O₂’. O₂’ preserves the intention of O₂. The input state of O₂’ is S⊙O₁.

Exclusion Transformation (ET)

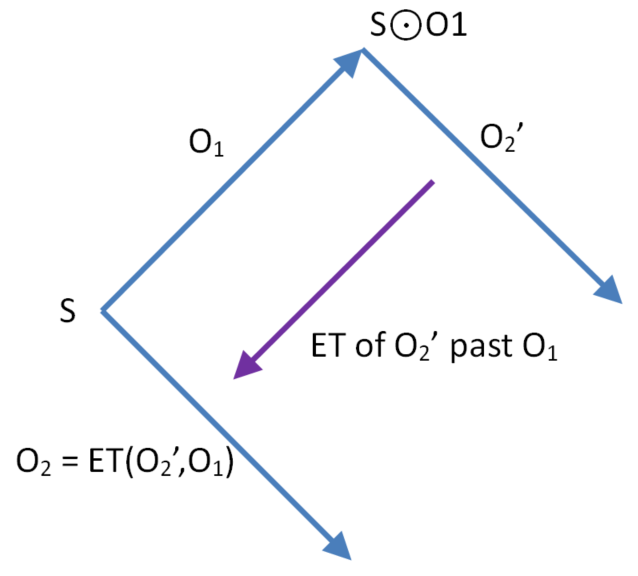
Let S be the input state of operation O₁ and let O₁,O₂’ be context serialised. The following diagram depicts the exclusion transform of O₂’ past O₁ to give O₂. O₂ preserves the intention of O₂’. The input state of O₂ is S.

TP1

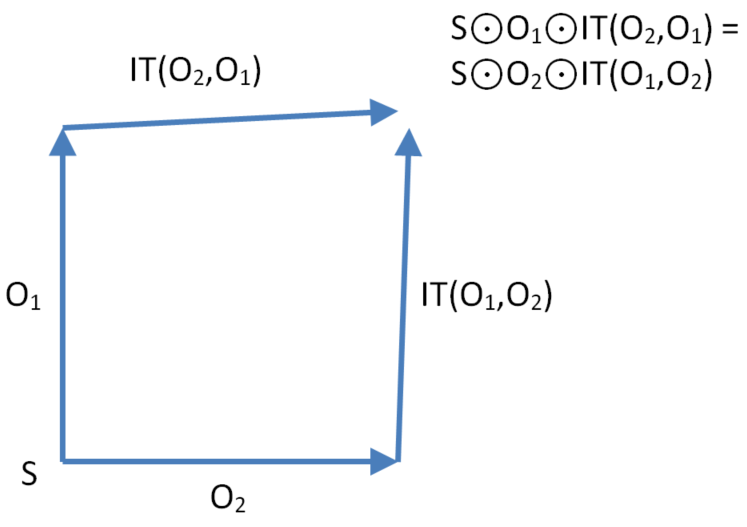
Transformation property TP1 ensures two sites converge to the same state

TP2

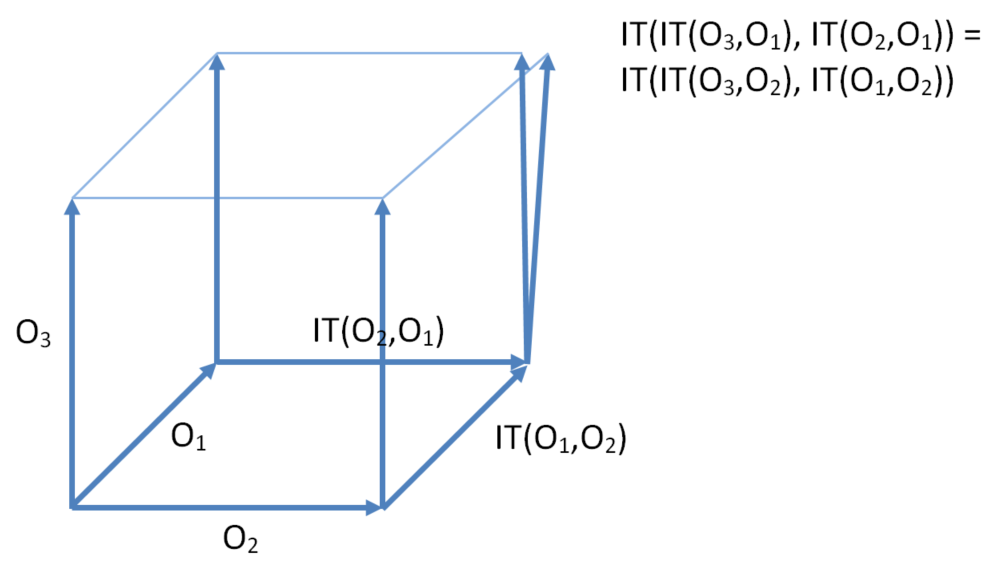
Let O₁, O₂ and O₃ be context equivalent operations. Transformation property TP2 means transforming operation O₃ either past O₁ then IT(O₂,O₁) or past O₂ then IT(O₁,O₂) gives the same result.

Sufficient conditions for convergence

TP1+TP2 implies convergence for different paths through the lattice

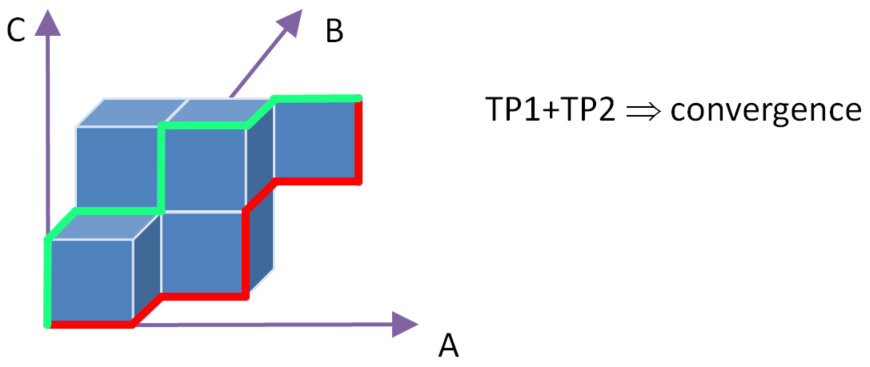
From an inductive definition of the lattice, In 1996 Ressel et al gave an inductive proof of convergence (using induction on the magnitude of the vector time).

OT approaches which don’t satisfy TP2

There are a number of approaches to OT which fail to satisfy condition TP2 (such as the approach used in Google Docs or Google Wave), and this imposes various limitations on the implementation:

• There can be unintuitive merge results e.g. the case of three operations on text where there’s an ambiguity for concurrent insertion positions on one of the faces. The solutions which fail to meet TP2 typically fail to respect a total order on insertions.
• Not robust:
• Can’t cope with server failure
• Requires transaction durability
• Network topology restrictions
• Poor interactivity
• No arbitrary branching and merging (configuration management)

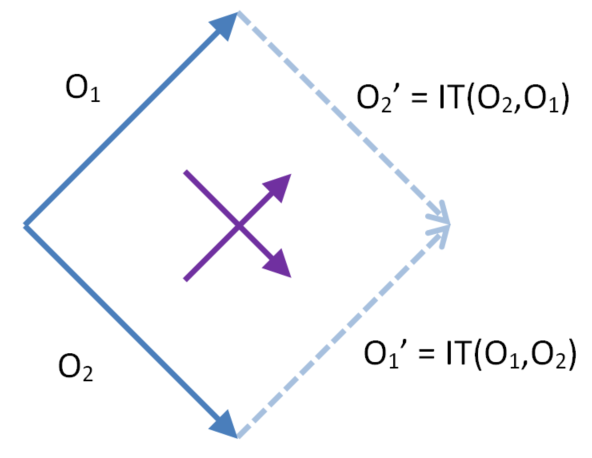
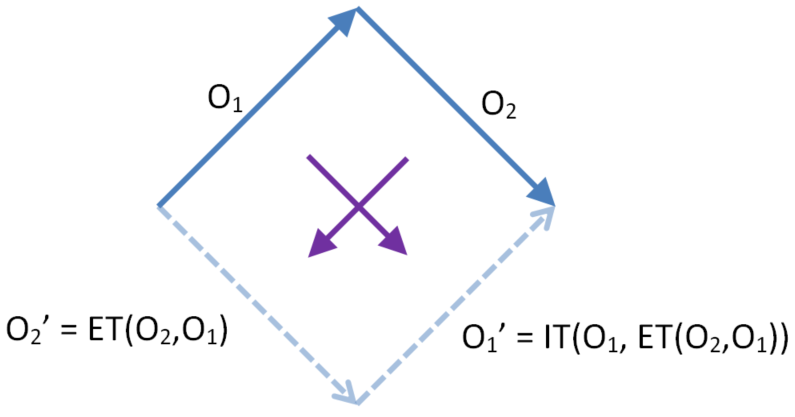
Dual IT

Let O₁ and O₂ be context equivalent operations. DualIT refers to the calculation of both inclusion transforms. In the diamond below the two operations on the left are transformed past each other to give the two operations on the right.

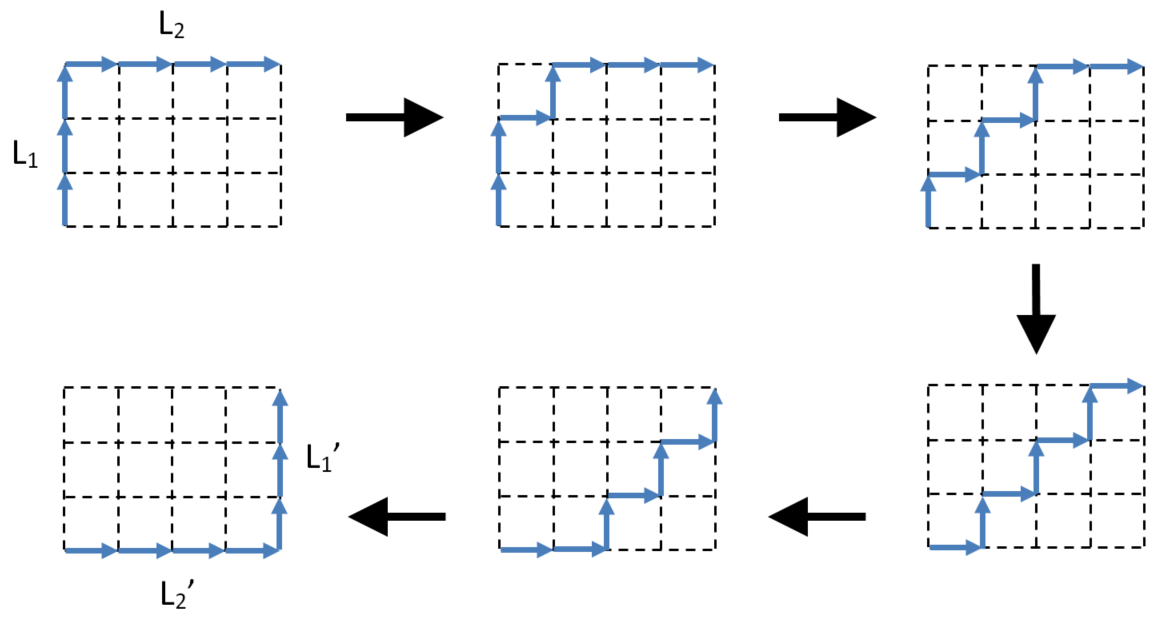
Similarly we can consider the dualIT of context equivalent lists of operations L₁, L₂ (we write L₁ || L₂ to mean the lists are concurrent, meaning ∀O₁∈L₁ ∀O₂∈L₂ O₁||O₂)

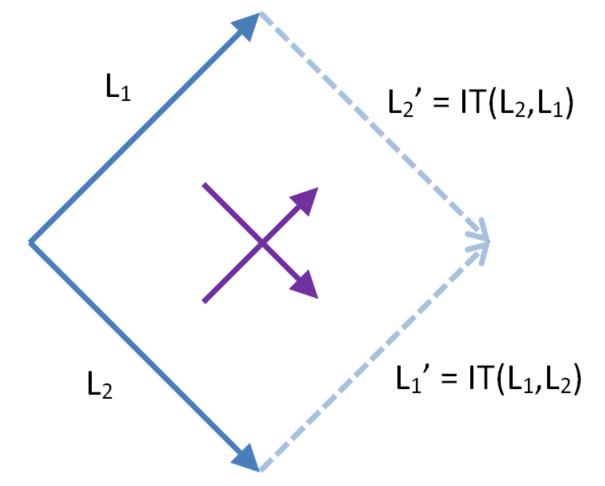
The following diagram shows how we can calculate IT(L₂,L₁) and IT(L₁,L₂). Unfortunately it has quadratic complexity, so it is not suitable for a practical implementation. In fact it implies the whole idea of using linear history buffers isn’t suitable for implementation.

Transpose

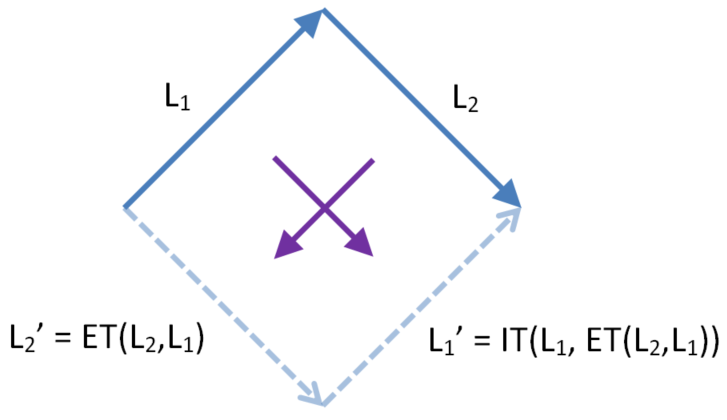
The transpose of context serialised operations O₁,O₂ is associated with applying them in the reverse order. In the following diagram the two operations on the top of the diamond are transformed to give the two operations on the bottom of the diamond:

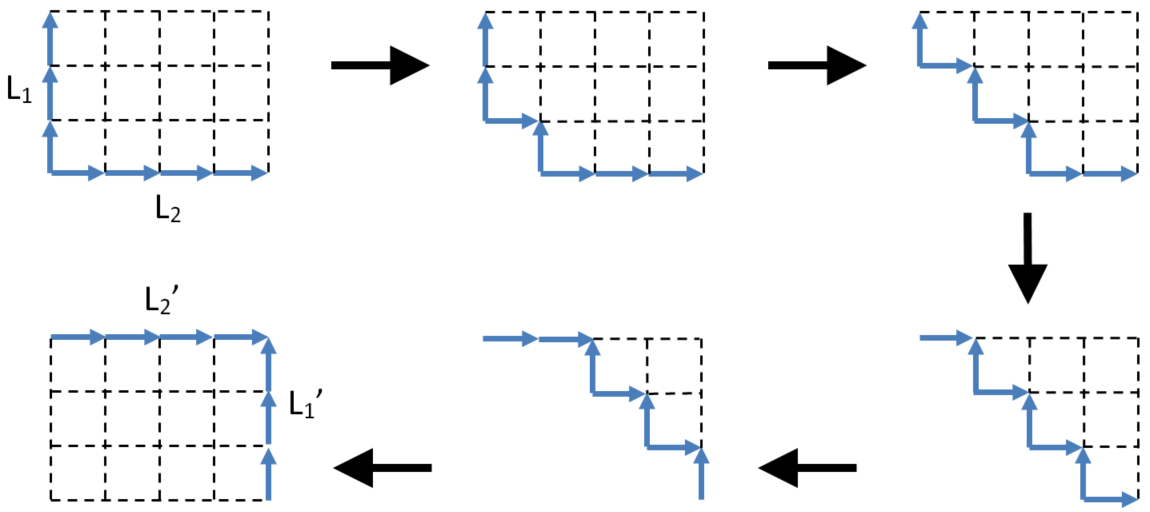
Similarly we can consider the transpose of context serialised lists of operations L₁, L₂

However just like DualIT the transpose of two lists is quadratic

History buffers of two sites

Consider the following Venn diagram depicting the sets of operations which have been applied so far at sites A and B

• The Ai are the operations unique to site A
• The Bi are the operations unique to site B
• The Ci are the operations they have in common

The set of operations in common represents a state that preserves causality. Also for the union of all operations

Consider that each site records the ordered list of operations it has applied so far (in the order they have been applied at that site). This list is called a History Buffer. For example:

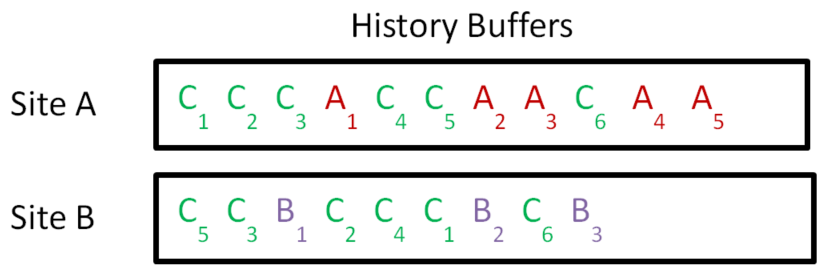
Site A has a mixture of the Ai and Ci. Site B has a mixture of the Bi and Ci.

Note that the common operations (the Ci) can be jumbled up with the Ai and Bi. Furthermore the Ci may not be in the same relative order in these two lists.

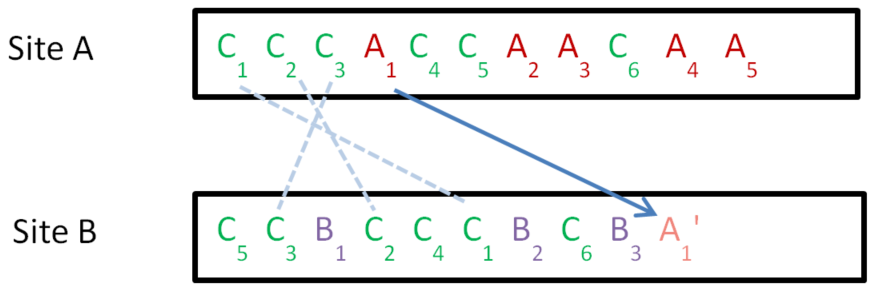
How do we synchronise the two sites? Consider for example that operation A₁ is sent to site B. The context for A₁ is the state in which {C₁ C₂ C₃} have been executed. We must somehow transform A₁ to A₁’ such that it can be appended to the end of site B’s history buffer.

Factorise

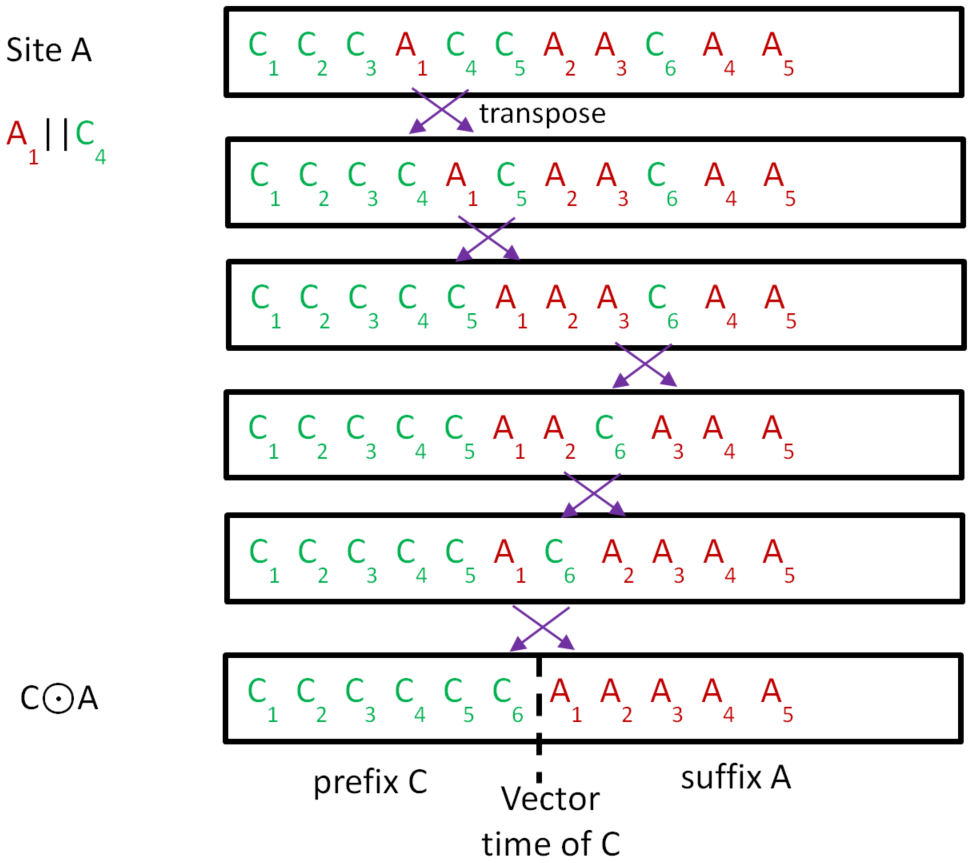
The history buffer of A has a mixture of C’s and A’s. We transpose adjacent pairs of Ai,Cj operations (i.e. where the Ai is to the left of the Cj) so all the C’s form a prefix and the A’s a suffix. This is possible because Ai || Cj. We can’t have Ai→Cj because that contradicts C preserving causality, and we can’t have Cj→Ai because Ai is to the left of Cj and the total order of the operations in a history buffer always respects the precedes partial order.

We call this a factorisation of the history buffer of site A with respect to a vector time V(C) to give C⊙A.

Synchronise two sites

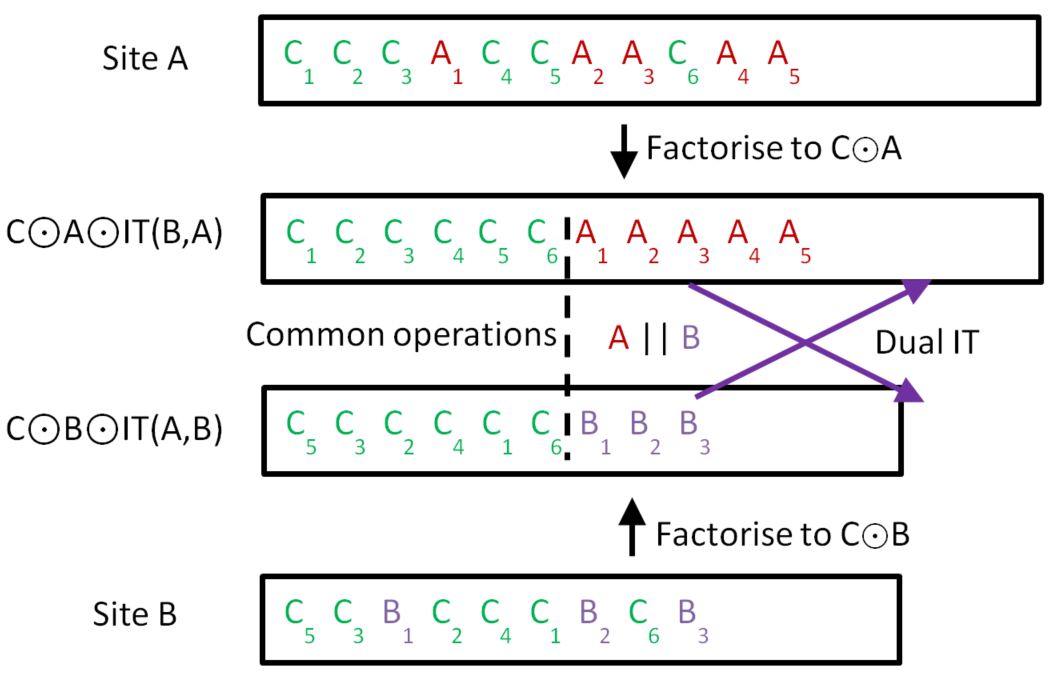
In the following diagram the history buffers of both site A and site B are factorised so that the common operations are in a prefix. That means that even though the common operations had been applied in a different order they result in the same state. Therefore the suffixes (the A’s and B’s) are applied in the same context and therefore a DualIT can be performed (noting that this is possible because A || B)

But too inefficient

We have described a solution described in the literature, but it is far too inefficient to be useful in a production system, because dualIT and factorisation are quadratic algorithms.

Fortunately linear approaches exist. CEDA uses algorithms that are linear in the number of operations that need to be merged. This typically allows for merging hours of works in a fraction of a second.