Infimum and Supremum (mathematics)

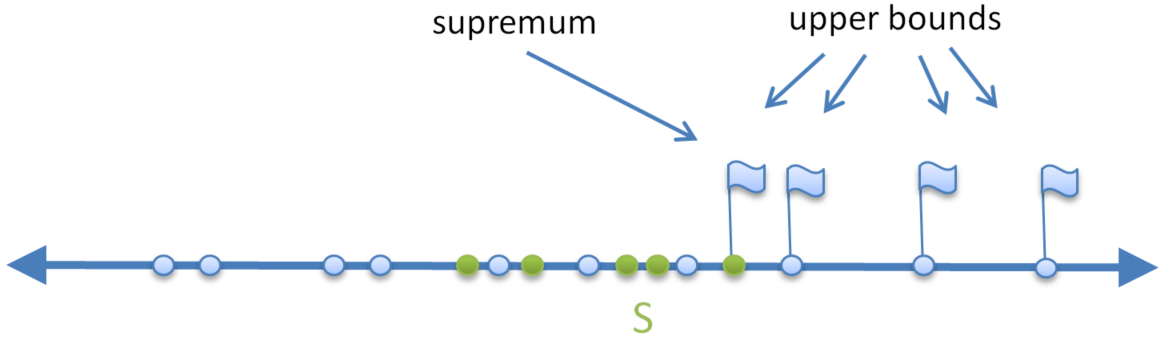
The infimum and supremum of a given subset of a partially ordered set (poset) are unique if they exist. The supremum is the lowest of all the upper bounds and the infimum is the greatest of all the lower bounds.

Let (P,≤) be a poset. Let S⊆P

u is an upper bound of S if (x∈S ⇒ x≤u)

s is the supremum of S if

• s is upper bound of S and
• u is upper bound of S ⇒ s≤u

For more information see the wikipedia article on infimum and supremum [].