Dependency Graph System (DGS)

The Dependency Graph System (DGS) is concerned with efficient recalculation of dependent variables (i.e. caches).

A data dependency between variables in and out is displayed as follows:

A significant part of software development relates to caching the results of time consuming calculations, and only recalculating caches when the inputs of the calculation have changed.

The following are some examples of dependent variables which represent caches:

The DGS works at the granularity of individual attributes within objects or tuples, or elements of arrays and maps. The following diagram shows the dependency graph amongst a number of objects. Note that it is only by looking at the graph at the fine-grained level of individual fields that we see that there are no cycles.

This system eliminates the need for the programmer to be concerned with using the observer pattern to update caches, and the need for attaching and detaching observers. Using the observer pattern is hard and error-prone.

Read barriers on data model fields and dependent nodes allow the dependency graph to be built and updated automatically.

The DGS is incremental in the sense that it only recalculates dependents that have been marked as dirty. It is lazy in the sense that a dependent variable is only calculated when its value is required.

Invalidation of caches

When inputs are changed, dependents are only marked as dirty (they are not recalculated immediately).

The dependency graph can change over time

The graph updates automatically as new dependencies appear and old dependencies disappear.

Early quiescence

The DGS detects early quiescence – which is where a recalculated variable ends up with the same value as it had before. In that case the DGS is able to avoid the recalculation of downstream nodes even though they had been marked as dirty.

Simple code example

CEDA features an elegant syntax for declaring dependent fields. Here is an example 


@import "Ceda/cxObject/DGNode.h"   // required when $deps are used

$struct X isa IObject
    model
    {
        int x1;
        int x2;
        int x3;
    }
{
    $dep int y1 = x1 + x2;
    $dep int y2 = y1 + x3;
};

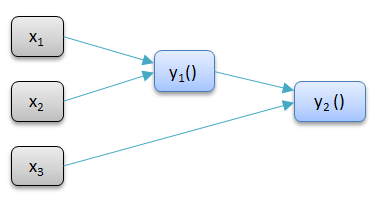
This means that y1 will cache the calculation of x1 + x2, and y2 will cache the calculation of y1 + x3. Note that this is not a practical example because these simple calculations would not normally need to be cached.

The associated dependency graph is as follows

The dependency graph is formed automatically as dependents are calculated. This makes it possible to automatically mark dependents as dirty as required. For example if x1 is changed then both y1 and y2 are marked as dirty.

In the following code 


void foo(X& x)
{
    std::cout << x.y2;
}

the read access to y2 may cause recalculation of y2 or y1 or both.

In general arbitrary code may be executed to calculate a dependent field value. This can access independent or dependent fields in the same object or in different objects. The DGS discovers the dependencies automatically at run time using read barriers on all the fields.

$cache functions

A more general alternative to $dep variables is to use $cache functions. Consider the following example where $cache functions are associated with the dependent variables y1 and y2

$cache functions with no input parameters are equivalent to $dep variables. 


$struct X isa IObject :
    model
    {
        int x1;
        int x2;
        int x3;
    }
{
    $cache int y1() const
    {
        return x1 + x2;
    };

    $cache int y2() const
    {
        return y1() + x3;
    };
};

$cache functions with input parameters

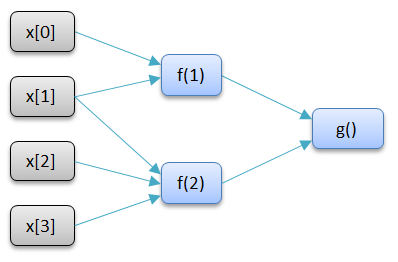
$cache functions can have one or more input parameters. In that case the calculated values are cached in a map keyed by the input parameters in the implementation. Cache map entries are evictable on an LRU basis. Each map entry actually represents a separate dependent node in the dependency graph that records in-nodes and out-nodes. Also like a $dep each map entry performs early quiescence testing (this can be turned off for all map entries by specifying $cache^). 


$struct X isa IObject :
    model
    {
        int x[4];
    }
{
    $cache int f(int a) const
    {
        return (a == x[1]) ? x[0] : std::max(x[2],x[3]);
    };

    $cache int g() const
    {
        return f(1) + f(2);
    }
};

Async $cache functions

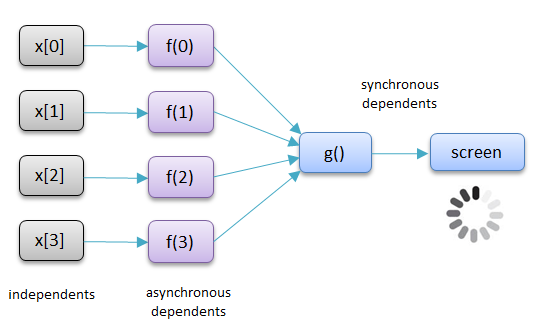
A modern UI should avoid showing wait cursors to the user, and where necessary perform time consuming activities such as computation in a worker thread. See Asynchronous UI. The DGS directly supports an asychronous UI by supporting dependent nodes which are updated asynchronously.

Asynchronous DGS nodes can have in-nodes and out-nodes just like synchronous nodes

$cache functions compose easily. Synchronous $cache functions can call asynchronous $cache functions and vice versa. 


$struct X isa IObject :
    model
    {
        int x[4];
    }
    public CWnd
{
    $cache <<async>> std::optional<int> f(int i) const 
        with int v = x[i]
    {
        return expensive_function(v);
    };

    $cache std::pair<int,int> g() const
    {
        int count = 0;
        int sum = 0;
        for (int i=0 ; i < 4 ; i++)
            if (auto r = f(i))
            {
                count++;
                sum += *r;
            }
        return { count, sum };
    }

    void draw() const
    {
        auto [count,sum] = g();
        if (count < 4) DrawSpinner();
        else           PrintSum(sum);
    }

    $dep void screen
        invalidate { CWnd::Invalidate(); }
        calc       { draw(); };

    void OnPaint() { screen(); }
};

Example: PersistStore

Conceptually the PersistStore provides both synchronous and asynchronous cache map functions to get the object with a given OID: 


class PersistStore
{
    $cache ptr<IPersistable> GetObject(OID oid) const;    

    $cache ptr<IPersistable> <<async>> AsyncGetObject(OID oid) const;
};

Example: multiresimage

The multiresimage demo uses an async $cache function to represent a cache updated asynchronously for the decompressed image tiles. 


class MultiResImage
{
    ...
    $cache <<async>> Image GetImageTile(int level, int x, int y) const
        with Jpeg jpeg = LoadJpegTile(level,x,y)
    {
        return DecompressJpeg(jpeg);
    }
};


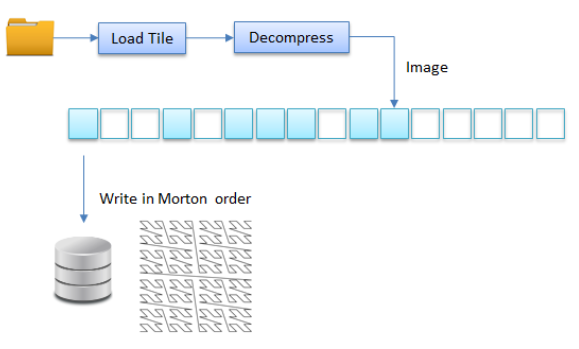
$cache <<async>> std::optional<Image> AsyncCalcTile(int i) const;

bool ProcessMoreTiles() const
{
    // add completed tiles to database in Morton order
    std::optional<Image> tile;
    while(index < count && tile=AsyncCalcTile(index))
    {
        database.AddTile(*tile);
        ++index;
    }
    if (index == count) return true;    // finished

    // fill pipeline with lookahead of 50
    for (int i=index+1 ; i < std::min(count,index+50) ; ++i)
        AsyncCalcTile(i);

    return false;   // not finished
}

$dep bool finished = ProcessMoreTiles();

Comparison to coroutines

Async $cache functions behave a bit like coroutines but without the complexity of co_await, co_yield and co_return.

When you call an async $cache function the calling thread doesnt block on the calculation, instead it just deals with a default constructed return value indicating not-yet-available. Your code that handles the returned value when it becomes available behaves like a continuation.

Detecting early quiescence

The basic form of the lazy evaluation approach requires invalidation of caches (i.e. marking caches as dirty) to propagate eagerly through the dependency graph. In other words, change notifications do nothing but invalidate caches, and this invalidation must immediately be propagated on to the dependents in a recursive fashion.

However, in practice it is common for calculations to produce results that don't change despite changes to the input. For example

Therefore the basic form of the lazy evaluation approach can be too eager in its cache invalidation strategy, leading to a great deal of unnecessary recalculation.

The DGS detects early quiescence – which is where a recalculated variable ends up with the same value as it had before. In that case the DGS is able to avoid the recalculation of downstream nodes even though they had been marked as dirty.

The solution is to introduce the concept of soft versus hard dirty states. When a node is changed it is marked as hard-dirty, and all dependent nodes are recursively marked as soft-dirty. ie only soft-dirtiness propagates immediately and eagerly through the dependency graph. When a node that is soft-dirty is read, it first calls the read barrier on all its immediate inputs to see whether they have really changed. If not then the soft-dirty status can be cleared without a need to recalculate the cache.

Definitions and terminology

There are two types of nodes in the dependency graph:

External agents represent external observers that have a liveliness contract - ie they are under contract to stay up to date - so therefore they are interested in receiving soft and hard invalidations from one or more nodes in the graph. As an example, an external agent may be associated with the output on the screen.

Note that nodes are finer grained than application objects. By making the dependency graph explicit we achieve dependency analysis within an application object as well as between application objects.

The dependency graph is a directed graph. It can be related to a data flow diagram.

In this example, n4, n5 are independent nodes. All the other nodes are dependent nodes. An external agent is "listening" to n1.

Nodes n6,n7 are involved in a cycle in the dependency graph. Cycles must be detected and dealt with appropriately at run time. They do not necessarily represent a design error in the program. For example, a system may allow end users to type in formulae at the nodes, making it quite easy for cycles to appear. This "error" must be dealt with at run time. In particular, it must not lead to a stack overflow!

Definition :

In the above diagram, the in-nodes of n2 are n4, n5. The out-nodes of n6 are n3, n7, n8.

Definition : A node is activated if there is a path in the dependency graph from the node to an external agent. Otherwise the node is deactivated.

In the above diagram, n8 is deactivated and all other nodes are activated.

Definition: We say that a node attaches to one of its in-nodes, in order to receive soft or hard invalidation notifications. Notifications are sent in the direction of the directed links in the dependency graph.

Requirements

Over time we allow for the following changes

Note that cycles can appear or disappear because of these changes. Large collections of nodes can transition between activated and deactivated.

Arbitrary many changes can accumulate before recalculation. All recalculation is dictated by external agents or other clients that call read barriers on nodes. A read barrier call may be issued on a deactivated node, although we don't expect that to be common.

The external agents are regarded as the ultimate source of any contractual obligations on the nodes. As such without agents, no dependency graph will be formed, and caches will always be assumed to be dirty.

A deactivated dependent node is irrelevant to the external agents. As such, we assume it is not necessary to keep its cache up to date. Therefore there is no need for it to attach to its in-nodes, or for any of its out-nodes to attach to it. In other words deactivated nodes take no part in the running of the dependency graph.

Note that conversely, a deactivated node is not able to trust its cache because it is not receiving any invalidation notifications. Despite this a deactivated node must still implement the read barrier function correctly. This will need to directly perform the calculation and return the result, without reading or writing the cache.

If there are no external agents, then no nodes will perform caching, or require notifications in order to invalidate those caches. Repeated calls to the read barrier on the nodes can be very expensive because no caching is performed.

Automatic building of the dependency graph

Unlike the observer pattern there is no need to explicitly attach and detach observers to subjects. Rather, this framework builds the dependency graph automatically by using read barriers on dependency graph nodes. This removes an error prone task and greatly simplifies the problem of writing an application.

The read barrier also allows the framework to take on responsibility for working out when to recalculate a cached value (because it is dirty)

Summary of advantages

The Dependency graph system features the following

The DGS checks all the boxes