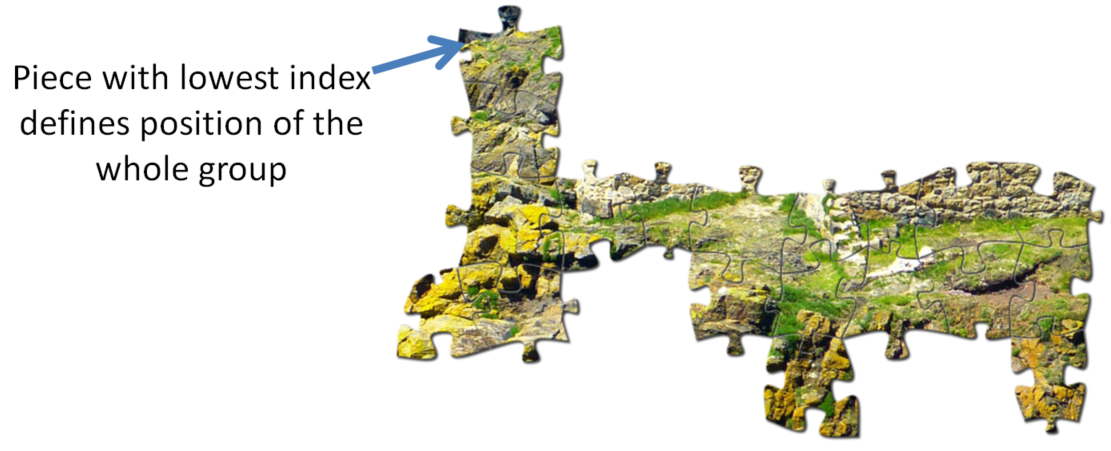
CEDA Jigsaw example

The jigsaw application allows many users to concurrently move the pieces around. Occasionally two people may drag the same piece with the mouse in different directions, and everyone sees it rapidly flicker between the two alternative positions as incoming operations to a given computer successively reassign the (x,y) location. This is an example of a "conflict" that is visually obvious and its resolution simply involves one person releasing the mouse.

The surprising feature supported by Operational Transformation (OT) is that some people can work on the jigsaw off-line and it is always possible to silently merge their work. This is achieved despite a model that keeps track of what pieces have been snapped together, and in fact the merging is performed in such a way that pieces that have been snapped together never come apart after merging.

Position constraints

The jigsaw is an interesting application from the point of view of the constraints on the jigsaw piece positions.

When pieces are snapped together there is a constraint on their relative positions. As the jigsaw is put together the constraints are increasing over time!

Properties:

• Any number of users can work independently, indefinitely and allow their work to be automatically merged
• Strong integrity constraints are imposed (whenever pieces are snapped together, their relative positions are forever fixed)
• As the jigsaw is put together more constraints are being imposed and the degrees of freedom are reducing
• Pieces that are snapped together can never come apart. The merge gives the union of what has been snapped together

Base representation

The following models are directly expressed in the CDM schema and provide the base representation of the jigsaw.

@def int NUMPIECES = 5000

$model+ Point
{
  int32 x;
  int32 y;
};

$model+ Piece
{
  Point pos;
  bool joinedOnRight;     // If set then implies this piece is connected to the piece on its immmediate right
  bool joinedOnBottom;    // If set then implies this piece is connected to the piece immmediately below
};

$model+ Jigsaw
{
  Piece pieces[NUMPIECES];
};

The base representation records the (x,y) of every piece, as well as information about which pieces have been snapped together.

There are no constraints defined on this base representation, so therefore the variables can be updated independently. The (x,y) positions of two pieces may be far apart even though they have been snapped together!

The base representation persists in the databases. It is replicated and synchronised by exchanging operations between sites. The OT merging algorithms only deal with this unconstrained base representation. It ensures all sites converge to the same base representation once all operations have been received and applied.

Derived representation

Each site has its own copy of the base representation in its local database, and from its base representation calculates a derived representation.

The constraints on the piece positions are imposed on the derived representation.

Although OT merging algorithms may need to make arbitrary decisions in order to resolve ambiguities because of symmetry, it is possible to interpret the underlying base representation in such a way that some activities (like snapping pieces together) take precedence over others (like moving pieces around).

The trick is to realise that integrity constraints that are imposed on the derived representation typically reduce the degrees of freedom in the model, and therefore there is an opportunity to resolve conflicts in favourable ways.

The integrity constraint imposed on the derived representation accounts for pieces that have been snapped together. This is achieved by ignoring some of the recorded piece positions in the base representation. As the jigsaw is being put together the number of degrees of freedom in the derived representation is steadily decreasing.

This reduction in the degrees of freedom means there isn’t a one-to-one correspondence between the base and derived representations. The mapping from base to derived can be described as many to one or non-injective.

For more information see the wikipedia article on an injective function [].

The derived sets of connected pieces

In the model each jigsaw piece has two boolean flags for whether that piece is connected to the piece to its immediate right, and the piece immediately below.

These boolean flags all together determine a partition of all the jigsaw pieces into sets of connected pieces.

The boolean flags are sufficient but not necessary for pieces to be connected. This avoids a complicated constraint on the boolean flags!

The derived piece position

The non-injective function

Point GetDerivedPiecePosition(int i);

returns the derived position of the i^th jigsaw piece.

For the given piece it finds the set of connected pieces containing that piece. The position of the set of connected pieces is determined by the piece in the set with the lowest index. The positions of the other pieces are offset as appropriate.